Il existe peu d’exercices de mathématiques traitant uniquement des algorithmes (qui devrait pourtant avoir un chapitre dédié, surtout vu la compréhension des élèves), voici donc quelques exercices de maths niveau terminale S sur les algorithmes :
L’article présente quelques exercices corrigés sur les algorithmes étant abordés en classes de première S et terminale S (ils peuvent toutefois être adaptés à d’autres filières). Si vous souhaitez reprendre des notions, Cliquez sur ce cours sur les algorithmes niveau lycée bac S.
Exercice 1
1/ Que fait l’algorithme ci-dessous ?
Variables
n, P, i, S
Algorithme
Afficher « Entrez le capital en euros : »
Lire S
Afficher « Entrez le taux : »
Lire P
Afficher « Entrez le nombre d’années : »
Lire n
Pour i de 1 jusqu’à n
S prend la valeur S*(1+P/100)
FinPour
Afficher S
2/ On a entré 1000 puis 10 puis 3. Qu’affiche l’algorithme ?
Corrigé 1
1/ L’algorithme calcule le montant final S d’une épargne définie par l’utilisateur à un taux P durant n années.
2/ 1000 x 1,103 = 1331.
Exercice 2
On considère l’algorithme suivant :
Variables
N, i, S
Algorithme
Afficher « Saisissez un nombre entier N : »
Saisir N
S reçoit la valeur 1
Pour i de 1 jusqu’à N
S reçoit S × i
FinPour
Afficher S
1) Tester cet algorithme pour N = 3 en donnant les résultats à chaque itération.
2) Indiquer à quelle ligne se fait l’initialisation et pourquoi est-elle importante.
Corrigé 2
1) Première boucle i = 1 ; S = 1
Deuxième boucle i = 2 ; S = 2
Troisième boucle i = 3 ; S = 6
Affichage final : 6
2) Ligne «S reçoit la valeur 1 », elle est importante sinon la boucle ne pourra pas se faire (la variable S ne serait pas définie).
Exercice 3
Ecrire un algorithme qui demande deux nombres à l’utilisateur et l’informe ensuite si leur produit est négatif ou positif (on laisse de côté le cas où le produit est nul). Attention toutefois : on ne doit pas calculer le produit des deux nombres.
Corrigé 3
Variables m, n en Entier
Début
Ecrire ”Entrez deux nombres : ”
Lire m, n
Si (m > 0 ET n > 0) OU (m < 0 ET n < 0)
Alors Ecrire ”Leur produit est positif”
Sinon Ecrire ”Leur produit est négatif”
Finsi
Fin
Exercice 4
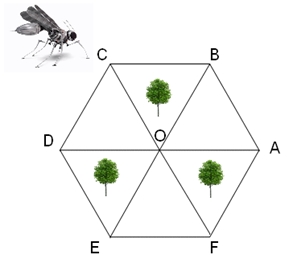
Un robot-insecte se déplace aléatoirement autour d’un parc hexagonal.
Il se déplace segment par segment de deux lettres adjacentes (il peut faire C –> B ou C –>O mais pas C à A).
1/ Ecrire un algorithme simulant son premier déplacement.
2/ Quelle est la probabilité d’arriver en A au bout de 2 déplacements.
Corrigé 5
1/ Le plus « simple » dans ce cas est de coder chaque lettre par un chiffre (ce qui sera plus facile à traiter avec un algorithme. (C = 1 ; D = 2 ; B = 3 ; O = 4)
Variable P entier
Choisir un entier aléatoire entre 2 et 4
P prend la valeur de cet entier aléatoire
Fin algorithme
2/ Faire un arbre (p = 1/6)
Exercice 6 : jeu du plus ou du moins
1/ Ecrire l’algorithme suivant : l’ordinateur choisit un entier au hasard entre 1 et 20000. L’utilisateur doit alors entrer un nombre. S’il entre un nombre plus petit que celui choisi par l’ordinateur on affiche « Plus grand ! », s’il entre un nombre plus grand que celui choisi par l’ordinateur on affiche « Plus petit !». Si c’est le bon nombre on affiche « Gagné ! ».
2/ Ajouter à l’algorithme un compteur pour savoir en combien de coups a gagné le joueur.
3/ Donner une méthode permettant de gagner rapidement en un minimum de coups (le nombre est maintenant choisi au hasard entre 0 et 1000).
Corrigé 6
1/
Début algorithme
i, nb_choisi et nb_joueur sont des entiers
nb_joueur prend la valeur 0
nb_choisi prend la valeur d’un entier aléatoire compris entre 1 et 20000
Tant que (nb_choisi <> nb_joueur)
Lire nb_joueur
Si (nb_joueur > nb_choisi)
Alors
Afficher « Plus grand ! »
Fin Si
Si (nb_joueur < nb_choisi)
Alors
Afficher « Plus petit !
Fin Si
Si (nb_joueur == nb_choisi)
Alors
Afficher « Gagné ! »
Fin Si
Fin Tant que
Fin algorithme
2/
Début algorithme
i, n, nb_choisi et nb_joueur sont des entiers
n prend la valeur 0
nb_joueur prend la valeur 0
nb_choisi prend la valeur d’un entier aléatoire compris entre 1 et 20000
Tant que (nb_choisi <> nb_joueur)
Lire nb_choisi
Si (nb_joueur > nb_choisi)
Alors
Afficher « Plus grand ! »
n prend la valeur n+1
Fin Si
Si (nb_joueur < nb_choisi)
Alors
Afficher « Plus petit !
n prend la valeur n+1
Fin Si
Si (nb_joueur == nb_choisi)
Alors
n prend la valeur n+1
Afficher « Gagné en »&n&« coups »
Fin Si
Fin Tant que
Fin algorithme
3/ On va utiliser cette technique : exemple avec 417 comme nombre choisi par l’ordinateur. Le joueur entre 912, l’algorithme affiche alors « Plus petit ! ». On calcule alors la moyenne de 912 et 0 = 456. L’algorithme affiche alors « Plus petit ». On calcule la moyenne entre 456 et 0 = 228. L’algorithme affiche « Plus Grand », on calcule la moyenne de 228 et 456 = 342. L’algorithme affiche « Plus Grand », on calcule alors la moyenne de 342 et 456 = 399. Et cætera et cætera, on appelle cette méthode la dichotomie.
Exercice algorithme bac S
Un groupe de 50 coureurs, portant des dossards numérotés de 1 à 50, participe à une course cycliste qui comprend 10 étapes, et au cours de laquelle aucun abandon n’est constaté. À la fin de chaque étape, un groupe de 5 coureurs est choisi au hasard pour subir un contrôle antidopage. Ces désignations de 5 coureurs à l’issue de chacune des étapes sont indépendantes. Un même coureur peut donc être contrôlé à l’issue de plusieurs étapes.
On considère l’algorithme ci-dessous dans lequel :
– « rand(1, 50) » permet d’obtenir un nombre entier aléatoire appartenant à l’intervalle [1; 50]
– l’écriture « x := y » désigne l’affectation d’une valeur y à une variable x.
Variables a, b, c, d, e sont des variables du type entier
Initialisation a := 0 ; b := 0 ; c := 0 ; d := 0 ; e := 0
Traitement
Tant que (a = b) ou (a = c) ou (a = d) ou (a = e) ou (b = c) ou (b = d) ou (b = e) ou (c = d) ou (c = e) ou (d = e)
Début du tant que
a := rand(1, 50); b := rand(1, 50); c := rand(1, 50); d := rand(1, 50); e := rand(1, 50)
Fin du tant que
Sortie
Afficher a, b, c d, e
(a) Parmi les ensembles de nombres suivants, lesquels ont pu être obtenus avec cet algorithme : L1 = {2, 11, 44, 2, 15} ; L2 = {8, 17, 41, 34, 6} ; L3 = {12, 17, 23, 17, 50} ; L4 = {45, 19, 43, 21, 18} ? (b) Que permet de réaliser cet algorithme concernant la course cycliste ?
N’oubliez pas que les algorithmes nous « entourent » (et c’est peu de le dire), en avoir un minimum de compréhension est important et ces exercices corrigés traitant des algorithmes pouvant être abordés au bac S vous permettront de vous entraîner (ou d’entraîner vos élèves).