Devoir sur les probabilités, les suites et la programmation Python pour les élèves de terminale spé maths. Un exercice qui reprend les notions de terminale spé maths, sur probabilités conditionnelles, suites géométriques, démonstration par récurrence et algorithme de seuil.
Énoncé du devoir probas – suites T°spé maths
Les résultats seront arrondis si nécessaire au centième.
Monsieur D, jeune professeur de mathématiques, est arrivé récemment dans un nouveau lycée. Il entame sa deuxième année. D’après son expérience dans ce lycée, il sait qu’il peut diviser ses journées en deux types : une bonne journée ou une mauvaise journée. De plus, s’il a passé une bonne journée le jour n, il passe une bonne journée le jour n+1 avec une probabilité égale à 0,9. S’il passe une mauvaise journée le jour n, il a 70% de chances de passer une mauvaise journée le jour n+1.
On note les évènements de la manière suivante :
- Jn : « Monsieur D passe une bonne journée le jour n ».
- Pn : « Monsieur D passe une mauvaise journée le jour n ».
On note jn la probabilité de l’évènement Jn. Et on s’intéresse dans un premier temps à la deuxième année de Monsieur D, depuis le jour de la rentrée. Le jour de la rentrée (jour 1), Monsieur D a passé une bonne journée. Monsieur D travaille le lundi, le mardi et le vendredi. S’il passe une bonne journée le vendredi, il passe un bon week-end et inversement.
1/ Monsieur D aimerait passer un bon weekend la semaine de la rentrée. Et pour cela il faut qu’il passe un bon vendredi. Quelle est la probabilité qu’il passe un bon weekend ?
2/ Monsieur D a finalement passé un mauvais weekend. Quelle est la probabilité qu’il ait passé un bon mardi la semaine de la rentrée ?
3/ a) Compléter l’arbre ci-dessous représentant la situation à un jour n quelconque et le jour suivant.
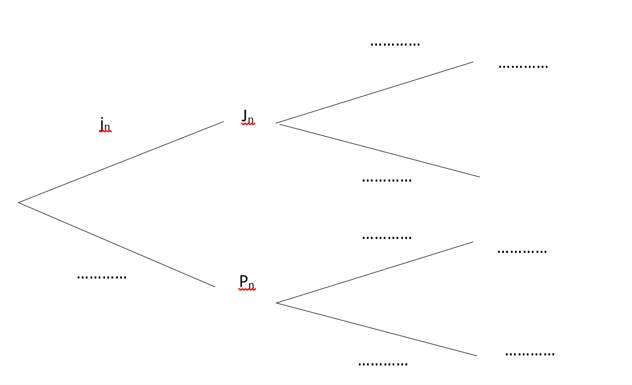
b) Montrer que jn+1 = 0,6 jn + 0,3
4/ a) Montrer que la suite un, définie pour tout entier naturel supérieur ou égal à 1, par un = jn – 0,75 est une suite géométrique.
b) Exprimer un en fonction de n, puis en déduire l’expression de jn en fonction de n.
c) À l’aube de se retraite, quelle sera la probabilité pour Monsieur D de passer une bonne journée (on considère dans ce cas vu l’âge de Monsieur D qu’il atteindra sa retraite quand n tend vers l’infini) ?
5/ Montrer par récurrence, que pour tout n ≥ 1, la suite jn est décroissante.
6/ Compléter le programme Python ci-dessous, pour qu’il affiche le rang correspondant au jour où la probabilité que Monsieur D passe une bonne journée devient inférieure à 0,75001.
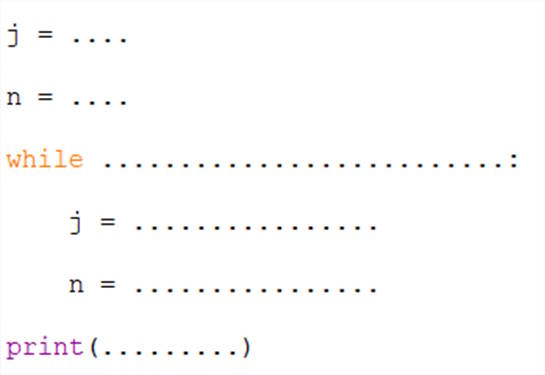
7/ Entrer ce programme à la calculatrice ou sur ordinateur et donner le résultat affiché. Retrouver ce résultat par le calcul.
Commentez pour toute question sur ce devoir sur les suites et probas pour des élèves de T° spé maths, ou son corrigé !