Tous les porteurs de lunettes apprécient maintenant son utilité : le traitement anti-reflet. Mais quelle est la composition de l’anti-reflet des lunettes et quel est le principe de fonctionnement de l’anti-reflet ?
Qu’est ce qu’un reflet ?
Lors de l’arrivée d’un flux lumineux (lumière) sur le verre d’une paire de lunettes, une partie du flux est transmis, il passe à travers le verre, ce qui permet ensuite à l’œil de voir l’image. Une autre partie peut être réfléchie : elle est à l’origine des reflets sur les lunettes.
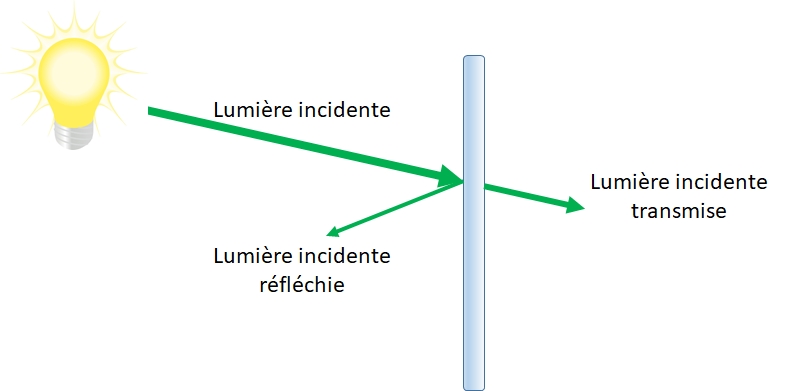
Comment de ce fait supprimer ce reflet ? C’est l’objet de cet article : détailler le principe de fonctionnement de l’anti-reflet des lunettes.
Principe de fonctionnement de l’anti-reflet des lunettes
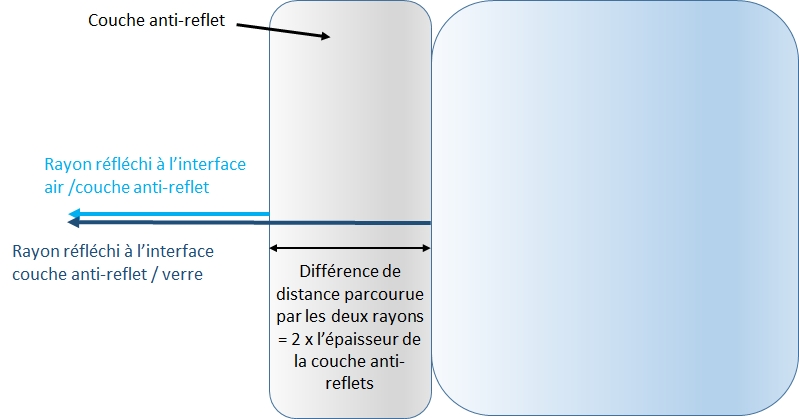
Pour supprimer ce reflet on va se servir d’un élément paradoxal : on va créer un autre reflet ! On cherche grâce à une couche supplémentaire sur la lunette à créer une autre réflexion de la lumière. Cette fois la réflexion est double comme sur ce schéma :
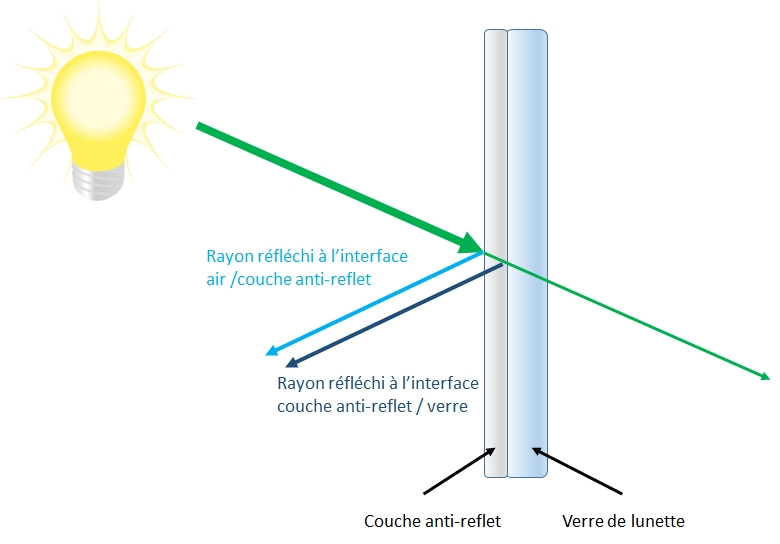
Le fonctionnement de l’anti-reflet des lunettes repose ensuite sur la physique des ondes. Ces quelques notions sont importantes pour la suite :
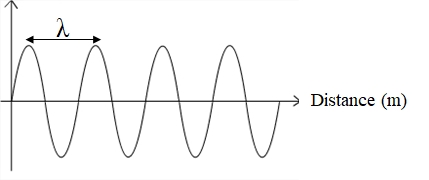
1/ La lumière peut être considérée, en partie, comme une onde sinusoïdale (figure 3).
2/ La distance entre deux points dans des états de perturbation identiques est appelée longueur d’onde (figure 3).
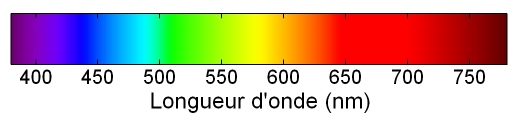
3/ La lumière visible a des longueurs d’onde allant d’environ 400 à 800 nm (figure 4).
4/ Lors de la superposition de deux ondes celles-ci s’ajoutent de façon algébrique (figure 5).

Les interférences
Lorsque les deux ondes s’ajoutent, on parle d’interférences, qui peuvent être constructives (à gauche) ou destructives (à droite). Dans le cas d’interférences avec des ondes lumineuses, si celles-ci sont constructives on observe un maximum de lumière. Si elles sont destructives on observe « rien » c’est à dire l’absence de lumière.
Le type d’interférence dépend de la « différence de marche » entre les deux ondes c’est à dire la différence de distance parcourue entre les deux ondes. Si la différence de marche est un multiple de la longueur d’onde, les interférences sont constructives, Si la différence de marche est égal à la moitié d’un demi-impair fois la longueur d’onde les interférences sont destructives, c’est par exemple le cas si la différence de marche est de λ/2 (schéma de droite) : lorsque la courbe rouge passe par un maximum la courbe bleue passe par un minimum : ceci conduit à une onde globale « plate ».
Pour que l’anti-reflet fonctionne il faut donc que l’onde réfléchie à l’interface air / couche anti-reflet, et celle réfléchie à l’interface couche / verre, soit en opposition de phase, afin de « s’annuler ». On note que l’onde fait l’aller-retour dans la couche anti-reflet : il faut donc au minimum que son épaisseur soit égale à λ/4. Ainsi la différence de distance parcourue est de 2 x λ/4 = λ/2 les interférences sont bien destructives ce qui a pour effet de ne plus rendre visible le reflet.
La prise en compte de l’indice de réfraction
Si l’on souhaite être plus précis il faut en réalité prendre en compte la différence de vitesse de la lumière entre l’air et la couche anti-reflet : celle-ci implique de prendre en compte l’indice de réfraction de la couche qu’on notera n. Ainsi l’épaisseur minimale de la couche est égal à λ/(4n). De même l’indice de réfraction de la couche est également fixé grâce aux équations de Maxwell qui implique que nCOUCHE = racine(nVERRE). Comme exemple on peut prendre le verre Crown. Utilisé pour la fabrication des lentilles, il a un indice de réfraction proche de 1,52, ce qui donne par le calcul racine(1,52) = 1,23. On utilise donc les matériaux ayant les indices de réfraction le plus proche possible de cette valeur comme le fluorure de magnésium d’indice de réfraction 1,38.

Le principe de fonctionnement de l’anti-reflet des lunettes repose donc sur la superposition d’une couche dite « anti-reflet » qui va permettre de créer une seconde onde lumineuse à l’interface couche / verre. Celle-ci va s’ajouter à celle créée à l’interface air / couche, et ainsi l’annuler grâce à des interférences destructives.
La composition de la couche anti-reflet des lunettes est généralement constituée de fluorure de magnésium.
Pour aller plus loin et pour les fans d’optique visitez la page Wikipédia sur les traitements anti-reflet de façon général.


Mouais… Avant cette invention je n’ai jamais été gêné par les reflets. Par contre à force de nettoyer les verres, la couche disparaît au bout de dix ans et laisse derrière plein de petits points. Donc je ne suis pas convaincu.
Bonjour,
merci pour le commentaire. Pour l’efficacité il y a pas mal de retours positifs (contrairement aux verres « anti lumière bleue » dont l’efficacité n’a pas été démontrée). Par contre effectivement cette couche est fragile et permet de vendre plus de lunettes… Et donc oui les lavages successifs détériorent la couche d’anti-reflet (particulièrement l’eau chaude).
Bonne journée !