Devoir sur les polynômes et les positions relatives de courbes pour les élèves de 1ère spé maths.
Le devoir aborde :
- exercice 1, la forme canonique sans utilisation des formules ;
- exercice 2, forme canonique avec les formules et forme factorisée à partir de la forme canonique ;
- exercice 3, les variations d’une fonction, sans utiliser les formules mais uniquement les propriétés sur les variations d’une fonction (si sur un intervalle I, a < b => f(a) < f(b) alors f est croissante sur I).
- exercice 4, études de la position relative de 2 courbes représentatives d’une fonction polynôme.
- exercices 5 et 6 qui sont des exercices plus complexes, à prise d’initiatives pour les élèves en avance.
Sujet du devoir positions relatives première spé maths (et polynômes)
Consignes du devoir sur les positions relatives et les polynômés première maths spécialité – Lycée en ligne Parti’Prof – J. Tellier
Durée 1h30 – Calculatrices autorisées
Exercice 1
Sans utiliser de formule, donner la forme canonique des deux polynômes ci-dessous :
A/ P(x) = x² – 4x + 1 B/ Q(x) = 3x² + 6x – 5
Exercice 2
Soit le polynôme R(x) = 4x² + 24x + 20.
a/ En utilisant les formules, donner la forme canonique de R(x).
b/ Donner la forme factorisée de R(x).
Exercice 3
Soient les fonctions f et g, définies sur par f(x) = 2(x – 4)² – 6 et g(x) = -3x² + 6x + 3.
Déterminer le sens de variation de f et g. Une attention particulière sera portée à la rédaction du raisonnement.
Exercice 4
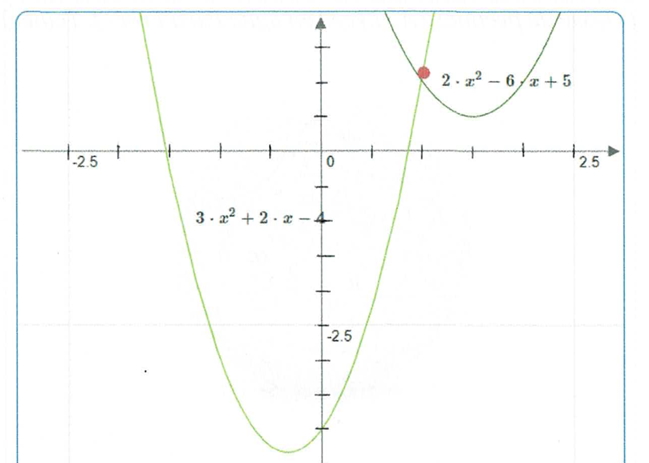
Soient les fonctions h et i, définies sur par h(x) = 3x² + 2x – 4 et i(x) = 2x² – 6x + 5. On note Ch et Ci leurs courbes représentatives dans un repère orthonormé. Voici les courbes tracées par Jade sur sa calculatrice :
a/ À l’aide du tracé effectué, conjecturer les coordonnées du ou des point(s) d’intersection de Ch et Ci.
b/ Montrer que h(x) – i(x) = 3 (x – 1)([1/3]x + 3)
c/ En déduire les coordonnées du ou des point(s) d’intersection de Ch et Ci. Commenter par rapport à la conjecture de la question a.
d/ Déterminer la position relative de Ch et Ci.
Exercice 5 (exercice à prise d’initiatives)
Soient les fonctions j et k, définies sur , par j(x) = 2x² – 1 et k(x) = x – 1. On note Cj et Ck leurs courbes représentatives dans un repère orthonormé.
Déterminer les positions relatives de Cj et Ck.
Exercice 6 (bonus, à faire uniquement si tous les autres sont terminés)
Soit la fonction m, définie sur , par m(x) = 2x² – 20x + 99/2. On note Cm sa représentation graphique dans un repère orthonormé.
Déterminer les coordonnées des points d’intersection de Cm avec l’axe des abscisses, sans utiliser le discriminant.
Toute trace de recherche « sensée » sera valorisée.
Et la version PDF :
Devoir positions relatives et polynômes maths première spécialité.
Petite vidéo rappel d’Yvan Monka pour l’étude des positions relatives si besoin : https://www.youtube.com/watch?v=EyxP5HIfyF4.
Commentez pour toute remarque ou question !