Ci-dessous un exemple de CCF de maths CAP (un seul exercice, les autres viendront dans d’autres articles) :
======== SUJET DU CCF DE MATHÉMATIQUES ========
Durée du CCF de maths CAP : 30 minutes / Calculatrice autorisée
Zoé travaille à temps partiel dans un restaurant avec les horaires suivants :
| Jour(s) | Horaires du midi | Horaires du soir |
| Mercredi, jeudi et vendredi | 11h à 13h | 18h à 22h |
| Samedi | 12h à 14h | 19h à 21h30 |
| Dimanche | 12h à 14h | 19h à 22h30 |
1/ Combien d’heures Zoé travaille-t-elle la journée du samedi ?
…………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………..
2/ Zoé ne travaille pas à temps plein (35h par semaine), mais à 80% (28h par semaine). Le salaire mensuel pour son poste à temps plein serait de 1400€ net.
Quel sera son salaire mensuel pour ce poste à 80% ?
…………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………..
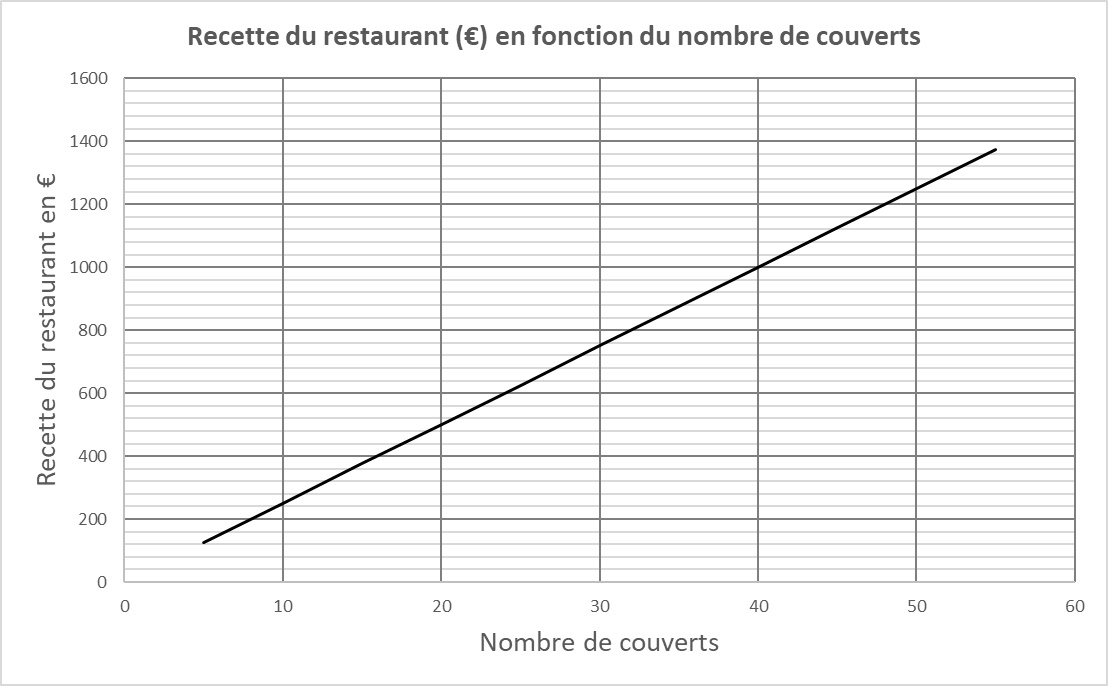
3/ Le patron du restaurant où travaille Zoé a pu réaliser quelques statistiques concernant sa recette moyenne (l’argent gagné par le restaurant), suivant le nombre de couverts (nombre de personnes ayant mangé dans le restaurant), qu’il a résumées sur la courbe ci-dessous :
À l’aide de cette courbe, répondre à ces questions :
a/ Quelle est la recette du restaurant s’il y a 40 couverts dans le restaurant (aucune justification attendue) ?
…………………………………………………………………………………………………………………..
b/ Combien de couverts faut-il pour avoir une recette de 500€ (aucune justification attendue)?
…………………………………………………………………………………………………………………..
c/ La recette du restaurant est-elle proportionnelle au nombre de couverts (justifier) ?
…………………………………………………………………………………………………………………..
d/ Est-il vrai que l’on dépasse 1200€ de recette pour environ 7 couverts (aucune justification attendue) ?
…………………………………………………………………………………………………………………..
4/ En appelant x le nombre de ouverts, Zoé a pu établir que la recette du restaurant était égale à 25 x.
Combien faudrait-il de couverts pour avoir une recette de 1450€ ?
…………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………..
5/ Le coût de fonctionnement du restaurant dépend également du nombre de couverts en salle. On sait que ce coût est donné par 5x + 200, avec x le nombre de couverts.
Aujourd’hui le coût de fonctionnement du restaurant a été de 415€.
Combien y-a-t-il eu de couverts ?
…………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………..
6/ Un travail est considéré « à temps plein » pour 35h par semaine. Cela correspond à 100%. On dit donc d’une personne travaillant 17,5h par semaine (la moitié de 35h) qu’elle travaille à 50%.
Pour des raisons personnelles, Zoé va maintenant travailler 21h par semaine.
Compléter cette phrase puis justifier :
Zoé travaillera à ……… %
Justifications :
…………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………..
========= GRILLE D’ÉVALUATION DU CCF DESTINÉE AUX ENSEIGNANTS ========
Liste des capacités, connaissances et attitudes évaluées
| Capacités | Détaillées dans le tableau ci-dessous. |
| Connaissances | Tableaux, graphiques, proportionnalité, situations du premier degré. |
| Attitudes | Savoir utiliser les différentes capacités vues en cours. |
Évaluation
| Compétences | Capacités | Questions | Appréciation du niveau d’acquisition |
| S’approprier | Lire un tableau à double entrée. | 1/ sur 1 point | |
| Analyser
Raisonner |
Déterminer graphiquement l’ordonnée d’un point d’une courbe, son abscisse étant donnée et inversement. | 3/a/ sur 1 point
3/b/ sur 1 point |
|
| Réaliser | Traiter des problèmes de pourcentage de la vie courante et de la vie professionnelle.
Résoudre un problème dont la formalisation conduit à une équation du type ax + b = c. |
2/ sur 1 point
6/ sur 1 point
4/ sur 1 point 5/ sur 1 point |
|
| Valider | Vérifier qu’une donnée est cohérente avec un graphique.
Vérifier qu’une situation est du type linéaire. |
3/d/ sur 1 point
3/c/ sur 1 point
|
|
| Communiquer | Phrases établies correctement, orthographe. | Toutes les questions sur 1 point | |
| /10 |
Pour information, lien vers le programme des classes de CAP en maths.