Devoir suites numériques – arithmétiques – géométriques première spé maths

Devoir de maths sur les suites numériques, ainsi que sur les suites arithmétiques et géométriques pour les élèves de première spé maths.

Le devoir (sans calculatrice) porte sur :

• exercice 1 : calculer les premiers termes d’une suite, définie de façon explicite et par récurrence.
• exercice 2 : représenter une situation donnée par une suite.
• exercice 3 : étudier le sens de variation d’une suite.
• exercice 4 : questions de cours sur les suites arithmétiques et géométriques.
• exercice 5 : calculer les termes d’une suite arithmétique et d’une suite géométrique.
• exercice 6 : retrouver la raison et le premier terme d’une suite arithmétique et géométrique.
• exercice 7 : conjecturer la limite de suites.
• exercice 8 : retrouver l’expression d’une suite à partir d’un programme Python.
• exercice 9 : exercice bilan sur les suites arithmétiques et géométriques. Sommes des termes de suites arithmétiques et géométriques.

Sujet du devoir sur les suites arithmétiques – géométriques Première Maths Spécialité

Consignes du devoir sur les suites numériques première maths spécialité – Lycée en ligne Parti’Prof – J. Tellier

Durée 1h30 – Calculatrices interdites

 

Exercice 1 (sans calculatrice)

Donner les 3 premiers termes de chacune des suites ci-dessous :

A/ u_n = 3 n + 1 avec \(n~\epsilon~\mathbb{N}\)

B / v_n = 2ⁿ – 1 avec \(n~\epsilon~\mathbb{N}\)

C/ u_n+1 = u_n + 7 et u₀ = 1 avec \(n~\epsilon~\mathbb{N}\)

 

Exercice 2 (sans calculatrice)

Dans chaque cas, définir une suite décrivant la situation :

A/ La population d’un village qui augmente de 10 habitants tous les ans avec une population initiale de 250 habitants.

u_n+1 = ………………………………………. et u₀ = ………….. avec \(n~\epsilon~\mathbb{N}\)

B / La suite des nombres pairs à partir de 2

u_n = ……………….. avec \(n~\epsilon~\mathbb{N}\)*

C/ Un loyer initial de 740€ qui augmente tous les ans de 1,5%.

…………………………………………………………………………………………………………………………………………………………

 

Exercice 3 (sans calculatrice)

Étudier le sens de variations des suites ci-dessous :

A/ a_n = 2n – 9

B/ b_n = \(\frac{n}{n+1}\)

C/ c_n = 2 + \(\frac{3}{n+1}\)

 

Exercice 4 (questions de cours – sans calculatrice)

Compléter le tableau de cours ci-dessous :

Suites arithmétiques Définition et expressions : Une suite arithmétique de raison r est définie par un+1 = ………………. On peut aussi exprimer un en fonction de n et du premier terme de la suite : un = ……………….

Suites géométriques Définition et expressions : Une suite géométrique de raison q est définie par vn+1 = ………………. On peut aussi exprimer vn en fonction de n et du premier terme de la suite : vn = ………………

 

Exercice 5 (sans calculatrice)

A/ (u_n) est une suite arithmétique de raison 2 et de premier terme u₀ = 9.

Calculer u₁ et u₁₂.

B/ (v_n) est une suite géométrique de raison 3 et de premier terme v₀ = 1.

Calculer v₁ et v₃.

 

Exercice 6 (sans calculatrice)

A/ (u_n) est une suite arithmétique avec u₃ = 5 et u₁₅ = 53.  Calculer sa raison et u₀.

B/ (v_n) est une suite géométrique avec v₁ = 6 et v₃ = 24. Calculer sa raison et v₀.

 

Exercice 7 (sans calculatrice)

Conjecturer la limite des suites ci-dessous :

A/ w_n = n + 2

B/ x_n = \(\frac{1}{n+1}\) + 1

C/ y_n = \(\frac{-1}{n²}\)

 

Exercice 8 (sans calculatrice)

Voici un programme Python :

Ce programme permet d’afficher les 10 premiers termes d’une suite (de u₀ à u₉).

Définir cette suite par son premier terme et une relation de récurrence.

 

Exercice 9 (sans calculatrice)

Vous venez d’être embauché(e) dans une entreprise. L’entreprise verse une prime de Noël à tous ses salariés avec 2 choix possibles :

• prime annuelle initiale de 1000 € augmentée de 250 € tous les ans (prime A)
• prime annuelle initiale de 1000 € augmentée de 10% tous les ans (prime B)

Une fois la prime A ou B choisie, cela n’est plus modifiable.

A/ Le montant de la prime A l’année « 0 » est de 1000 €. Quel sera le montant de la prime l’année 1 puis l’année 2 ? Par quel type de suite peut-on représenter la prime A ?

B/ Le montant de la prime B l’année « 0 » est de 1000 €. Quel sera le montant de la prime l’année 1 puis l’année 2 ? Par quel type de suite peut-on représenter la prime B ?

C/ Calculer le montant de la prime A l’année 10.

D/ Calculer le montant de la prime B l’année 10.

 

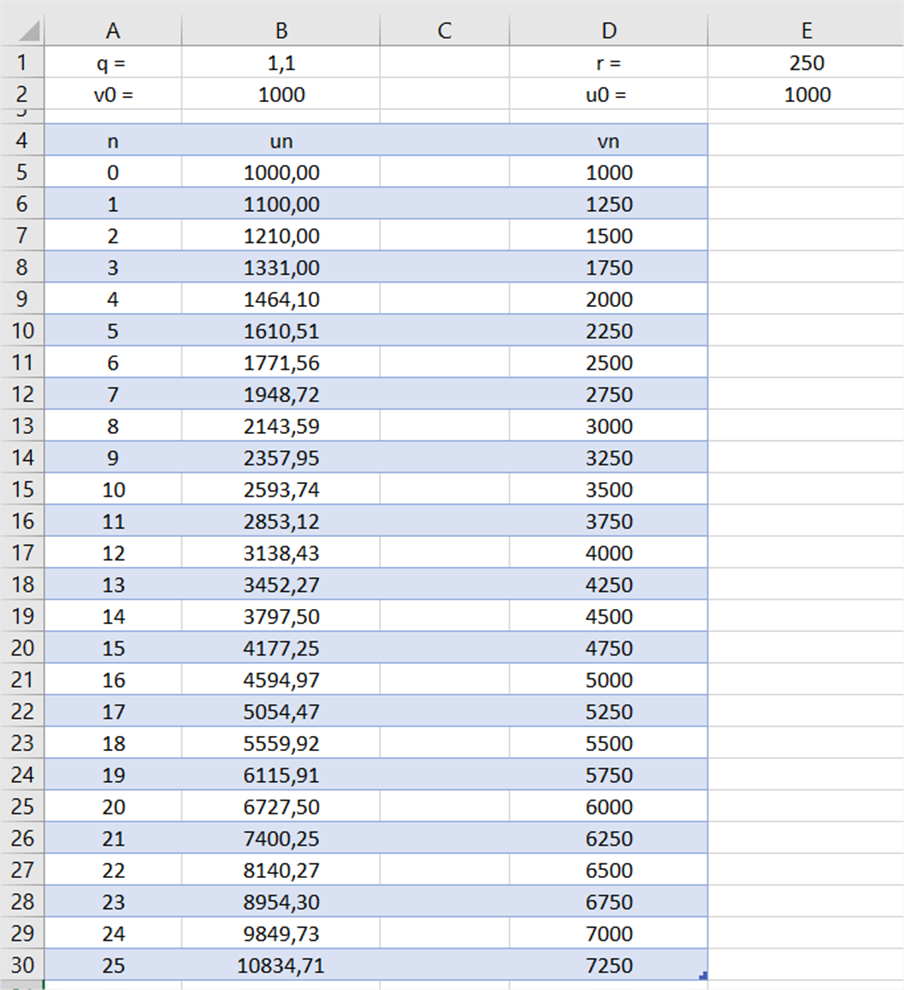
On a calculé le montant des primes annuelles (notée u_n pour la prime A et v_n pour la prime B) à l’aide d’un tableur, dont une capture d’écran est présentée ci-dessous :

E/ À partir de quelle année le montant annuel de la prime A dépasse celui de la prime B ?

F/ Pour un salarié restant 26 ans dans l’entreprise, quel est le choix le plus avantageux (on souhaite donc savoir le montant total des primes touchées sur 26 ans pour la prime A et la prime B) ?

Aide aux calculs :        1,1²⁶  11,918              8250 x 26 = 214500

 

Et la version PDF :

Devoir suites numériques – arithmétiques – géométriques première spé maths

 

Commentez pour toute question ou remarque sur ce devoir !